Leyes de los gases ( 2 DE BGU) REALIZAR LA TAREA PROPUESTA AL FINAL DE ESTE TEXTO

Leyes de los gases

• CONCEPTOS 
• Presión: es la cantidad de fuerza aplicada sobre una superficie. La unidad de presión en SI es el pascal (Pa) pero para el análisis matemático de las leyes de los gases se usa la unidad de atmosfera (atm); 1 atm es igual a 101325 Pa.
• Volumen: es el espacio ocupado por una cierta cantidad de masa y se expresa en litros (L).
• Temperatura: es la medida de la agitación interna de las partículas de gas y se expresa en unidades kelvin (K). Para transformar centígrados a kelvin, sólo tenemos que sumar 273.
• Moles: es la cantidad de masa del gas . Se representa con la letra n y sus unidades son moles.

¿Qué es un gas ideal?

Para poder aplicar las leyes de los gases se debe definir qué es un gas ideal. Un gas ideal es un gas teórico compuesto de partículas que se mueven al azar y que no interactúan entre ellas. Los gases en general se comportan de manera ideal cuando se encuentran a altas temperaturas y bajas presiones. Esto es debido a la disminución de las fuerzas intermoleculares.

Cuando un gas se encuentra a muy baja temperatura y/o bajo condiciones de presión extremadamente altas ya no se comporta de forma ideal. Bajo estas condiciones las leyes de los gases no se cumplen.

Condiciones estándar

Nos referimos a condiciones estándar cuando una sustancia se encuentra a 1 atm de presión y 273 K de temperatura (es decir, 0ºC) tiene un volumen de 22,4 L por mol de sustancia.

Ley de Boyle

La presión absoluta y el volumen de una masa dada de un gas confinado son inversamente proporcional, mientras la temperatura no varíe dentro de un sistema cerrado.

Robert Boyle (1627-1691) dedujo esta ley en 1662. La presión y el volumen de un gas ideal están inversamente relacionados: cuando uno sube el otro baja y viceversa.

La ley de Boyle se expresa matemáticamente como:

o

En esta ley solo existen dos variables: presión y volumen. Se asume que la temperatura del gas y el número de moléculas del gas en la jeringa no cambia.

Ejemplo

Si el gas en una jeringa está originalmente a 1 atm y el volumen es 5 mL, luego presión por volumen (PV) sera igual 5 atm-mL. Si el émbolo se empuja hasta reducir el volumen de 2,5 mL, entonces la presión tendrá que aumentar hasta 2 atm, de manera de mantener constante PV.

Ley de Charles

A presión constante, el volumen de una dada cantidad de un gas ideal aumenta al aumentar la temperatura.

Jacques Alexandre Charles (1746-1823) hizo el primer vuelo en globo inflado con hidrógeno en 1783 y formuló la ley que lleva su nombre en 1787.

La ley de Charles se expresa matemáticamente como:

ó

Cuando se aplica la ley de Charles, se debe usar la temperatura absoluta. Para convertir la temperatura de ºC a kelvin (K) se suma 273. Ejemplo:

20 ºC + 273= 293 K

100 ºC + 273= 373 K

Ejemplo

Una llanta de un vehículo se llena con 100 L (V₁) de aire a 10ºC. Luego de rodar varios kilómetros la temperatura sube a 40ºC (T₂) ¿Cuánto será el volumen de aire (V₂) en la llanta?

Ley de Gay-Lussac

La presión es directamente proporcional a la temperatura.

Joseph Louis Gay-Lussac (1778-1850)

La ley de Gay-Lussac se puede expresar matemáticamente como:

ó

Al aumentar la temperatura de un gas confinado en un recipiente, aumenta la energía cinética de las moléculas del gas y, como consecuencia, las colisiones con las paredes del contenedor. El aumento de la frecuencia de colisiones resulta en el aumento de la presión.

EJERCICIOS RESUELTOS 

Ejercicio Nº 1

A presión de 17 atm, 34 L de un gas a temperatura constante experimenta un cambio ocupando un volumen de 15 L ¿Cuál será la presión que ejerce?

Solución:

Primero analicemos los datos:

Tenemos presión (P 1 ) = 17 atm

Tenemos volumen (V 1 ) = 34 L

Tenemos volumen (V 2 ) = 15 L

Claramente estamos relacionando presión (P) con volumen (V) a temperatura constante, por lo tanto sabemos que debemos aplicar la Ley de Boyle y su ecuación (presión y volumen son inversamente proporcionales):

Reemplazamos  con los valores conocidos

Colocamos a la izquierda de la ecuación el miembro que tiene la incógnita (P 2 ) y luego la despejamos:

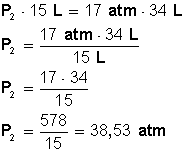
Respuesta:

Para que el volumen baje hasta los 15 L, la nueva presión será de 38,53 atmósferas.

Ejercicio Nº 2

¿Qué volumen ocupa un gas a 980 mmHg, si el recipiente tiene finalmente una presión de 1,8 atm y el gas se comprime a 860 cc?

Solución:

Analicemos los datos que nos dan:

Tenemos presión (P 1 ) = 980 mmHg

Tenemos presión (P 2 ) = 1,8 atm

Tenemos volumen (V 2 ) = 860 cc

Lo primero que debemos hacer es uniformar las unidades de medida.

Recuerda que la presión debe estar o en atmósferas (atm) o en milímetros de Mercurio (mmHg), pero no en ambas, y que el volumen debe estar en litros (L).

P 1 = 980 mmHg (lo dejamos igual)

P 2 = 1,8 atm lo multiplicamos por 760 y nos da 1.368 mmHg. Esto porque 1 atmósfera es igual a 760 mmHg

V 2 = 860 centímetros cúbicos lo expresamos en litros dividiendo por mil, y nos queda V 2 = 0,86 L (recuerda que un litro es igual a mil centímetros cúbicos).

Como vemos, de nuevo estamos relacionando presión (P) con volumen (V), a temperatura constante, por ello aplicamos la ecuación que nos brinda la Ley de Boyle (presión y volumen son inversamente proporcionales):

Reemplazamos con los valores conocidos

Ahora despejamos V 1

Respuesta:

A una presión de 980 mmHg dicho gas ocupa un volumen de 1,2 L (1.200 centímetros cúbicos).

Ejercicio Nº 3

A presión constante un gas ocupa 1.500 (ml) a 35º C ¿Qué temperatura es necesaria para que este gas se expanda hasta alcanzar los 2,6 L?

Solución:

Analicemos los datos:

Tenemos volumen (V 1 ) = 1.500 ml

Tenemos temperatura (T 1 ) = 35º C

Tenemos volumen (V 2 ) = 2,6 L

Lo primero que debemos hacer es uniformar las unidades de medida.

Recuerda que el volumen (V) debe estar en litros (L) y la temperatura (T) en grados Kelvin.

V 1 = 1.500 mililitros (ml), lo dividimos por 1.000 para convertirlo en 1,5 L

T 1 = 35º C le sumamos 273 para dejarlos en 308º Kelvin (recuerda que 0º C es igual a 273º K) (Nota: En realidad son 273,15, pero para facilitar los cálculos prescindiremos de los decimales).

V 2 = 2,6 L, lo dejamos igual.

En este problema estamos relacionando volumen (V) con temperatura (T), a presión constante, por lo tanto aplicamos la fórmula que nos brinda la Ley de Charles (volumen y temperatura son directamente proporcionales).

Reemplazamos con los valores conocidos

Desarrollamos la ecuación:

Primero multiplicamos en forma cruzada, dejando a la izquierda el miembro con la incógnita, para luego despejar T 2 :

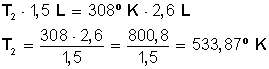
Entonces, para que 1,5 L expandan su volumen hasta 2,6 L hay que subir la temperatura hasta 533,78º Kevin, los cuales podemos convertir en grados Celsius haciendo la resta 533,87 − 273 = 260,87 º C.

Respuesta:

Debemos subir la temperatura hasta los 260,87º C.

                                                TAREA 

1.  REALIZAR UN RESUMEN DE CADA UNA DE LAS LEYES EN SU CUADERNO

2. REALIZAR LOS SIGUIENTES EJERCICIOS EN UN UNA HOJA PERFORADA.

1. En un recipiente de 1,5 m3 se introduce un gas a 3,7 × 105 Pa. Si disminuimos la presión a 8,3 × 104 Pa

sin variar la temperatura, ¿qué volumen ocupará?

2. Un gas ocupa 0,4 m3 a 305 K y 1,82 × 106 Pa. Calcula a qué presión estará sometido si doblamos el

volumen y mantenemos la temperatura constante.

3. En un experimento que se desarrolla a presión constante, un gas a 275 K ocupa 6 L. Construye la gráfica

del volumen ocupado por el gas en función de la temperatura para valores comprendidos entre

200 y 400 K.

4. Un gas que se encuentra a una temperatura de 298 K ocupa un volumen de 5 × 10-3 m3.

—¿Qué volumen ocupará si aumentamos su temperatura en 50 K?