Leyes de los gases ( 2 de BGU) Realizar cinco ejercicios cambiando de datos

Ejercicios sobre las Leyes de los gases

Ejercicio Nº 1

A presión de 17 atm, 34 L de un gas a temperatura constante experimenta un cambio ocupando un volumen de 15 L ¿Cuál será la presión que ejerce?
Solución:
Primero analicemos los datos:
Tenemos presión (P ₁ ) = 17 atm
Tenemos volumen (V ₁ ) = 34 L
Tenemos volumen (V ₂ ) = 15 L
Claramente estamos relacionando presión (P) con volumen (V) a temperatura constante, por lo tanto sabemos que debemos aplicar la Ley de Boyle y su ecuación (presión y volumen son inversamente proporcionales):

Reemplazamos  con los valores conocidos

Colocamos a la izquierda de la ecuación el miembro que tiene la incógnita (P ₂ ) y luego la despejamos:

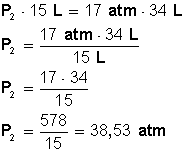
Respuesta:
Para que el volumen baje hasta los 15 L, la nueva presión será de 38,53 atmósferas.

Ejercicio Nº 2

¿Qué volumen ocupa un gas a 980 mmHg, si el recipiente tiene finalmente una presión de 1,8 atm y el gas se comprime a 860 cc?
Solución:
Analicemos los datos que nos dan:
Tenemos presión (P ₁ ) = 980 mmHg
Tenemos presión (P ₂ ) = 1,8 atm
Tenemos volumen (V ₂ ) = 860 cc
Lo primero que debemos hacer es uniformar las unidades de medida.
Recuerda que la presión debe estar o en atmósferas (atm) o en milímetros de Mercurio (mmHg), pero no en ambas, y que el volumen debe estar en litros (L).
P ₁ = 980 mmHg (lo dejamos igual)
P ₂ = 1,8 atm lo multiplicamos por 760 y nos da 1.368 mmHg. Esto porque 1 atmósfera es igual a 760 mmHg
V ₂ = 860 centímetros cúbicos lo expresamos en litros dividiendo por mil, y nos queda V ₂ = 0,86 L (recuerda que un litro es igual a mil centímetros cúbicos).
Como vemos, de nuevo estamos relacionando presión (P) con volumen (V), a temperatura constante, por ello aplicamos la ecuación que nos brinda la Ley de Boyle (presión y volumen son inversamente proporcionales):

Reemplazamos con los valores conocidos

Ahora despejamos V ₁

Respuesta:
A una presión de 980 mmHg dicho gas ocupa un volumen de 1,2 L (1.200 centímetros cúbicos).

Ejercicio Nº 3

A presión constante un gas ocupa 1.500 (ml) a 35º C ¿Qué temperatura es necesaria para que este gas se expanda hasta alcanzar los 2,6 L?
Solución:
Analicemos los datos:
Tenemos volumen (V ₁ ) = 1.500 ml
Tenemos temperatura (T ₁ ) = 35º C
Tenemos volumen (V ₂ ) = 2,6 L
Lo primero que debemos hacer es uniformar las unidades de medida.
Recuerda que el volumen (V) debe estar en litros (L) y la temperatura (T) en grados Kelvin.
V ₁ = 1.500 mililitros (ml), lo dividimos por 1.000 para convertirlo en 1,5 L
T ₁ = 35º C le sumamos 273 para dejarlos en 308º Kelvin (recuerda que 0º C es igual a 273º K) (Nota: En realidad son 273,15, pero para facilitar los cálculos prescindiremos de los decimales).
V ₂ = 2,6 L, lo dejamos igual.
En este problema estamos relacionando volumen (V) con temperatura (T), a presión constante, por lo tanto aplicamos la fórmula que nos brinda la Ley de Charles (volumen y temperatura son directamente proporcionales).

Reemplazamos con los valores conocidos

Desarrollamos la ecuación:
Primero multiplicamos en forma cruzada, dejando a la izquierda el miembro con la incógnita, para luego despejar T ₂ :

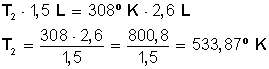
Entonces, para que 1,5 L expandan su volumen hasta 2,6 L hay que subir la temperatura hasta 533,78º Kevin, los cuales podemos convertir en grados Celsius haciendo la resta 533,87 − 273 = 260,87 º C.
Respuesta:
Debemos subir la temperatura hasta los 260,87º C.

Ejercicio Nº 4

¿Qué volumen ocupa un gas a 30º C, a presión constante, si la temperatura disminuye un tercio (1/3) ocupando 1.200 cc?
Solución:
Analicemos los datos:
Tenemos temperatura (T ₁ ) = 30º C
Tenemos temperatura (T ₂ ) = 30º C menos 1/3 = 20º C
Tenemos volumen (V ₂ ) = 1.200 cc
Lo primero que debemos hacer es uniformar las unidades de medida.
Recuerda que el volumen (V) debe estar en litros (L) y la temperatura (T) en grados Kelvin.
T ₁ = 30º C le sumamos 273 para dejarlos en 303º Kelvin (recuerda que 0º C es igual a 273º K)
T ₂ = 20º C le sumamos 273 para dejarlos en 293º Kelvin (recuerda que 0º C es igual a 273º K) (Nota: En realidad son 273,15, pero para facilitar los cálculos prescindiremos de los decimales).
V ₂ = 1.200 cc los dividimos por 1.000 para convertirlo en 1,2 L.
En este problema estamos relacionando volumen (V) con temperatura (T) a presión constante, por lo tanto aplicamos la fórmula que nos brinda la Ley de Charles (volumen y temperatura son directamente proporcionales).

Reemplazamos con los valores conocidos

Desarrollamos la ecuación:
Primero multiplicamos en forma cruzada, dejando a la izquierda el miembro con la incógnita, para luego despejar V ₁ :

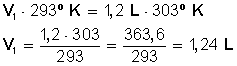
Respuesta:
A 30º C (303º K) el gas ocupa un volumen de 1,24 L (1.240 cc)

Ejercicio Nº 5

A volumen constante un gas ejerce una presión de 880 mmHg a 20º C ¿Qué temperatura habrá si la presión aumenta en 15 %?
Analicemos los datos:
Tenemos presión P ₁ = 880 mmHg
Tenemos presión P ₂ = 880 mmHg más el 15 %  = 880 +132= 1.012 mmHg
Tenemos temperatura T ₁ = 20º C
Lo primero que debemos hacer es uniformar las unidades de medida.
Recuerda que la temperatura (T) debe estar en grados Kelvin, y que la presión (P) puede estar solo en atm o solo en mmHg en una misma ecuación.
P ₁ = 880 mmHg, lo dejamos igual
P ₂ = 1.012 mmHg lo dejamos igual
T ₁ = 20º C le sumamos 273 para dejarlos en 293º Kelvin (recuerda que 0º C es igual a 273º K) (Nota: En realidad son 273,15, pero para facilitar los cálculos prescindiremos de los decimales).
En este problema estamos relacionando presión (P) con temperatura (T) a volumen (V) constante, por lo tanto aplicamos la fórmula que nos brinda la Ley de Gay-Lussac (presión y temperatura son directamente proporcionales).

Reemplazamos con los valores conocidos

Desarrollamos la ecuación:
Primero multiplicamos en forma cruzada, dejando a la izquierda el miembro con la incógnita, para luego despejar P ₂ :

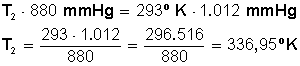
Respuesta:
Si aumentamos la presión en 15 % el gas quedará a una temperatura de 336,95º K, los cuales equivalen a 63,95º C.  (336,95 − 273 = 63,95º C).

Ejercicio Nº 6

Cuando un gas a 85º C y 760 mmHg, a volumen constante en un cilindro, se comprime, su temperatura disminuye  dos tercios (2/3) ¿Qué presión ejercerá el gas?
Solución
Analicemos los datos:
Tenemos presión P ₁ = 760 mmHg
Tenemos temperatura T ₁ = 85º C
Tenemos temperatura T ₂ = 85º C menos 2/3 = 85 − 56,66 = 28,34º C
Lo primero que debemos hacer es uniformar las unidades de medida.
Recuerda que la temperatura (T) debe estar en grados Kelvin, y que la presión (P) puede estar solo en atm o solo en mmHg en una misma ecuación.
P ₁ = 760 mmHg, lo dejamos igual
T ₁ = 85º C le sumamos 273 para quedar en 358º K (recuerda que 0º C es igual a 273º K) (Nota: En realidad son 273,15, pero para facilitar los cálculos prescindiremos de los decimales).
T ₂ = 28,34º C le sumamos 273 para quedar en 301,34º K
En este problema estamos relacionando presión (P) con temperatura (T) a volumen (V) constante, por lo tanto aplicamos la fórmula que nos brinda la Ley de Gay-Lussac (presión y temperatura son directamente proporcionales).

Reemplazamos con los valores conocidos

Desarrollamos la ecuación:
Primero multiplicamos en forma cruzada, dejando a la izquierda el miembro con la incógnita, para luego despejar P ₂ :

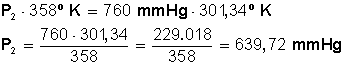
Respuesta
La presión baja hasta los 639,72 mmHg, equivalentes 0,84 atmósfera  (1 atm = 760 mmHg)