Reactivo limitante y rendimiento teórico ( SEGUNDO INTENSIVO) REALICE UN MAPA CONCEPTUAL

 

Reactivo limitante y rendimiento teórico

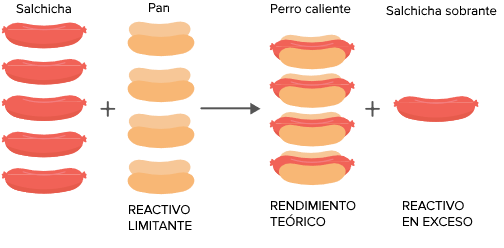
Es un acertijo clásico: tenemos cinco salchichas y cuatro panes. ¿Cuántos perritos calientes podemos hacer?

Una reacción con cinco salchichas y cuatro panes reaccionaría para formar cuatro perritos calientes completos y sobraría una salchicha. Los panes son el reactivo limitante y la salchicha que sobra es el reactivo en exceso. Los cuatro perritos calientes completos son el rendimiento teórico.

Suponiendo que las salchichas y los panes se combinan en una tasa de uno a uno, estaremos limitados por el número de panes porque es lo que se nos va a acabar primero. En esta situación poco ideal llamaríamos a los panes el reactivo limitante.

En una reacción química, el reactivo limitante es el reactivo que determina cuánto producto se va a obtener. A veces decimos que los otros reactivos están en exceso porque va a sobrar algo cuando el reactivo limitante se haya utilizado por completo. La cantidad máxima de producto que se puede producir se llama el rendimiento teórico. En el caso de las salchichas y los panes, nuestro rendimiento teórico son los cuatro perritos calientes completos, puesto que tenemos cuatro salchichas. ¡Pero ya es suficiente de perritos calientes! En el siguiente ejemplo vamos a identificar el reactivo limitante y vamos a calcular el rendimiento teórico de una reacción química real.

Consejo para resolver el problema: el primer paso y el más importante para hacer cualquier cálculo de estequiometría —como encontrar el reactivo limitante o el rendimiento teórico— es empezar con una ecuación balanceada. Como nuestros cálculos utilizan proporciones basadas en los coeficientes estequiométricos, nuestras respuestas serán incorrectas si los coeficientes no están bien.

Ejemplo 1: encontrar el reactivo limitante

En la siguiente reacción, ¿cuál es el reactivo limitante si empezamos con 2.80g de $\text {Al}$start text, A, l, end text y 4.25g de $\text {Cl}_2$start text, C, l, end text, start subscript, 2, end subscript?

$2 \text{Al}(s)+ 3\text{Cl}_2(g) \rightarrow 2 \text{AlCl}_3(s)$2, start text, A, l, end text, left parenthesis, s, right parenthesis, plus, 3, start text, C, l, end text, start subscript, 2, end subscript, left parenthesis, g, right parenthesis, right arrow, 2, start text, A, l, C, l, end text, start subscript, 3, end subscript, left parenthesis, s, right parenthesis

Primero revisemos si nuestra reacción está balanceada: tenemos dos átomos de $\text{Al}$start text, A, l, end text y seis de $\text{Cl}$start text, C, l, end text a ambos lados de la flecha, ¡así que estamos listos! En este problema conocemos la masa de ambos reactivos y nos gustaría saber cuál va a ser el primero en agotarse. Lo que haremos será convertir todo a moles, después vamos a utilizar la relación estequiométrica de la reacción balanceada para encontrar el reactivo limitante.

Paso 1: convertir las cantidades a moles.

Podemos convertir las masas de $\text {Al}$start text, A, l, end text y $\text {Cl}_2$start text, C, l, end text, start subscript, 2, end subscript a moles usando los pesos moleculares:

$\text{moles de Al}=2.80 \,\cancel{\text {g de Al}} \times \dfrac{1\,\text{mol de Al}}{26.98 \,\cancel{\text {g de Al}}}= 1.04 \times 10^{-1}\,\text {mol de Al}~~~~~~~~~~~~~~~~\text{(Convertir los g de Al a moles de Al).}$start text, m, o, l, e, s, space, d, e, space, A, l, end text, equals, 2, point, 80, start cancel, start text, g, space, d, e, space, A, l, end text, end cancel, times, start fraction, 1, start text, m, o, l, space, d, e, space, A, l, end text, divided by, 26, point, 98, start cancel, start text, g, space, d, e, space, A, l, end text, end cancel, end fraction, equals, 1, point, 04, times, 10, start superscript, minus, 1, end superscript, start text, m, o, l, space, d, e, space, A, l, end text, space, space, space, space, space, space, space, space, space, space, space, space, space, space, space, space, start text, left parenthesis, C, o, n, v, e, r, t, i, r, space, l, o, s, space, g, space, d, e, space, A, l, space, a, space, m, o, l, e, s, space, d, e, space, A, l, right parenthesis, point, end text

$\text{moles de Cl}_2=4.25 \,\cancel{\text {g de Cl}_2} \times \dfrac{1\,\text{mol de Cl}_2}{70.90 \,\cancel{\text {g de Cl}_2}}= 5.99 \times 10^{-2} \,\text {mol de Cl}_2~~~~~~~~~\text{(Convertir g de Cl}_2 \text{ a moles de Cl}_2)$start text, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, equals, 4, point, 25, start cancel, start text, g, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, times, start fraction, 1, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, divided by, 70, point, 90, start cancel, start text, g, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, end fraction, equals, 5, point, 99, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, space, space, space, space, space, space, space, space, space, start text, left parenthesis, C, o, n, v, e, r, t, i, r, space, g, space, d, e, space, C, l, end text, start subscript, 2, end subscript, start text, space, a, space, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, right parenthesis

Paso 2: encontrar el reactivo limitante mediante la relación estequiométrica.

Ahora que las cantidades que conocemos están en moles, hay varias formas de encontrar el reactivo limitante. Aquí te vamos a enseñar tres métodos. Todos dan la misma respuesta, así que puedes escoger el que más te guste. Los tres métodos usan la relación estequiométrica de formas ligeramente distintas.

MÉTODO 1: el primer método consiste en calcular la relación molar verdadera de los reactivos y compararla con la relación estequiométrica de la ecuación balanceada.

$\text{Proporción real}=\dfrac{\text{moles de Al}}{\text{moles de Cl}}_2=\dfrac{1.04 \times 10^{-1}\,\text {mol de Al}}{5.99 \times 10^{-2} \,\text {mol de Cl}_2}=\dfrac{1.74 \,\text{mol de Al}}{\text{1 mol de Cl}_2}$start text, P, r, o, p, o, r, c, i, o, with, \', on top, n, space, r, e, a, l, end text, equals, start fraction, start text, m, o, l, e, s, space, d, e, space, A, l, end text, divided by, start text, m, o, l, e, s, space, d, e, space, C, l, end text, end fraction, start subscript, 2, end subscript, equals, start fraction, 1, point, 04, times, 10, start superscript, minus, 1, end superscript, start text, m, o, l, space, d, e, space, A, l, end text, divided by, 5, point, 99, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end fraction, equals, start fraction, 1, point, 74, start text, m, o, l, space, d, e, space, A, l, end text, divided by, start text, 1, space, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end fraction

La proporción real nos dice que tenemos 1.74 moles de $\text{Al}$start text, A, l, end text por cada 1 mol de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript. En comparación, la relación estequiométrica de la reacción balanceada se muestra a continuación:

$\text{Relación estequiométrica}=\dfrac{2 \,\text{mol de Al}}{3 \,\text {mol de Cl}_2}=\dfrac{0.67 \,\text{mol de Al}}{1\,\text{mol de Cl}_2}$start text, R, e, l, a, c, i, o, with, \', on top, n, space, e, s, t, e, q, u, i, o, m, e, with, \', on top, t, r, i, c, a, end text, equals, start fraction, 2, start text, m, o, l, space, d, e, space, A, l, end text, divided by, 3, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end fraction, equals, start fraction, 0, point, 67, start text, m, o, l, space, d, e, space, A, l, end text, divided by, 1, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end fraction

Esto significa que necesitamos, al menos, 0.67 moles de $\text{Al}$start text, A, l, end text por cada mol de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript. Debido a que nuestra proporción real es mayor que nuestra relación estequiométrica, tenemos más $\text{Al}$start text, A, l, end text del que necesitamos para reaccionar con cada mol de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript. Por lo tanto, $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript es nuestro reactivo limitante y $\text{Al}$start text, A, l, end text está en exceso.

MÉTODO 2: un método más del tipo de prueba y error para averiguar cuál es el reactivo limitante consiste en escoger uno de los reactivos —no importa cuál— y simular que ese es el reactivo limitante. Así podemos calcular los moles del otro reactivo con base en los moles del que se supone que es nuestro reactivo limitante. Por ejemplo, si simulamos que $\text {Al}$start text, A, l, end text es el reactivo limitante, calcularíamos la cantidad requerida de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript como sigue:

$\text {moles de Cl}_2=1.04 \times 10^{-1}\,\cancel{\text {mol de Al} }\times \dfrac{3\,\text {mol de Cl}_2}{2 \,\cancel{\text {mol de Al}}}=1.56\times 10^{-1}\,\text{mol de Cl}_2$start text, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, equals, 1, point, 04, times, 10, start superscript, minus, 1, end superscript, start cancel, start text, m, o, l, space, d, e, space, A, l, end text, end cancel, times, start fraction, 3, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, divided by, 2, start cancel, start text, m, o, l, space, d, e, space, A, l, end text, end cancel, end fraction, equals, 1, point, 56, times, 10, start superscript, minus, 1, end superscript, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript

Con base en estos cálculos, necesitaríamos $1.56\times 10^{-1}\,\text{moles de Cl}_2$1, point, 56, times, 10, start superscript, minus, 1, end superscript, start text, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript si $\text{Al}$start text, A, l, end text fuera el reactivo limitante. Como tenemos $5.99 \times 10^{-2} \,\text {moles de Cl}_2$5, point, 99, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, que es menos que $1.56\times 10^{-1}\,\text{moles de Cl}_2$1, point, 56, times, 10, start superscript, minus, 1, end superscript, start text, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, nuestros cálculos nos dicen que se nos agotaría el $\text {Cl}_2$start text, C, l, end text, start subscript, 2, end subscript antes de que todo el $\text{Al}$start text, A, l, end text reaccionara. Por lo tanto, el $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript es nuestro reactivo limitante.

MÉTODO 3: en el tercer método se emplea el concepto del mol de reacción. Un mol de reacción se utiliza como unidad cuando reaccionan los moles de los coeficientes de la ecuación balanceada. La definición puede sonar un poco confusa, pero el siguiente ejemplo ayuda a ponerla en contexto. En la reacción que estamos trabajando diríamos que obtenemos 1 mol de reacción cuando 2 moles de $\text{Al}$start text, A, l, end text reaccionan con 3 moles de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript para producir 2 moles de $\text{AlCl}_3$start text, A, l, C, l, end text, start subscript, 3, end subscript, lo que también podemos escribir como

$1\,\text{mol de reacción}=2\,\text{mol de Al}=3\,\text{mol de Cl}_2=2\,\text{mol de AlCl}_3$1, start text, m, o, l, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, end text, equals, 2, start text, m, o, l, space, d, e, space, A, l, end text, equals, 3, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, equals, 2, start text, m, o, l, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript

Podemos usar la igualdad anterior para construir proporciones que nos ayuden a convertir los moles de cada reactivo a los moles de la reacción:

$1.04 \times 10^{-1}\,\cancel{\text {mol de Al}}\times \dfrac{1\,\text{mol-reacción}}{2 \,\cancel{\text {mol de Al}}}= 5.20 \times 10^{-2}\,\text {mol-reaccion}~~~~~~~~~~~~\text{(Convertir mol de Al a mol-reacción).}$1, point, 04, times, 10, start superscript, minus, 1, end superscript, start cancel, start text, m, o, l, space, d, e, space, A, l, end text, end cancel, times, start fraction, 1, start text, m, o, l, negative, r, e, a, c, c, i, o, with, \', on top, n, end text, divided by, 2, start cancel, start text, m, o, l, space, d, e, space, A, l, end text, end cancel, end fraction, equals, 5, point, 20, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, negative, r, e, a, c, c, i, o, n, end text, space, space, space, space, space, space, space, space, space, space, space, space, start text, left parenthesis, C, o, n, v, e, r, t, i, r, space, m, o, l, space, d, e, space, A, l, space, a, space, m, o, l, negative, r, e, a, c, c, i, o, with, \', on top, n, right parenthesis, point, end text

$5.99 \times 10^{-2} \,\cancel{\text {mol de Cl}_2} \times \dfrac{1\,\text{mo de reacción}}{3 \,\cancel{\text {mol de Cl}_2}}=2.00 \times 10^{-2} \,\text {mol de reacción}~~~~~~~~\text{(Convertir moles de Cl}_2 \text{ a moles de reacción)}$5, point, 99, times, 10, start superscript, minus, 2, end superscript, start cancel, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, times, start fraction, 1, start text, m, o, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, end text, divided by, 3, start cancel, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, end fraction, equals, 2, point, 00, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, end text, space, space, space, space, space, space, space, space, start text, left parenthesis, C, o, n, v, e, r, t, i, r, space, m, o, l, e, s, space, d, e, space, C, l, end text, start subscript, 2, end subscript, start text, space, a, space, m, o, l, e, s, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, right parenthesis, end text

Entre más moles de reacción haya, la reacción va a ocurrir más veces. Entonces, el reactivo con el menor número de moles de reacción es el reactivo limitante puesto que la reacción con ese reactivo puede llevarse a cabo menos veces. Podemos notar que este método también verifica que el $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript es nuestro reactivo limitante porque produce $2.00 \times 10^{-2} \,\text {moles de reacción}$2, point, 00, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, e, s, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, end text, que es menos que los $5.20 \times 10^{-2}\,\text {moles de reacción}$5, point, 20, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, e, s, space, d, e, space, r, e, a, c, c, i, o, with, \', on top, n, end text del $\text{Al}$start text, A, l, end text.

Ejemplo 2: calcular el rendimiento teórico

Ahora que sabemos cuál es el reactivo limitante, podemos usar esa información para contestar la siguiente pregunta:

¿Cuál es el rendimiento teórico de $\text {AlCl}_3$start text, A, l, C, l, end text, start subscript, 3, end subscript que puede producir la reacción cuando empezamos con 4.25 g de $\text {Cl}_2$start text, C, l, end text, start subscript, 2, end subscript, nuestro reactivo limitante?

Podemos usar los moles del reactivo limitante junto con la relación estequiométrica de la reacción balanceada para calcular el rendimiento teórico. Los coeficientes de la reacción balanceada nos dicen que por cada 3 moles de $\text{Cl}_2$start text, C, l, end text, start subscript, 2, end subscript deberíamos obtener 2 moles de $\text{AlCl}_3$start text, A, l, C, l, end text, start subscript, 3, end subscript. Por lo tanto, el rendimiento teórico en moles es

$\text{Rendimiento teórico en moles}=5.99 \times 10^{-2}\,\cancel{\text {mol de Cl}_2} \times \dfrac{2\,\text {mol de AlCl}_3}{3 \,\cancel{\text {mol de Cl}_2}}=3.99\times 10^{-2}\,\text {mol de AlCl}_3$start text, R, e, n, d, i, m, i, e, n, t, o, space, t, e, o, with, \', on top, r, i, c, o, space, e, n, space, m, o, l, e, s, end text, equals, 5, point, 99, times, 10, start superscript, minus, 2, end superscript, start cancel, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, times, start fraction, 2, start text, m, o, l, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript, divided by, 3, start cancel, start text, m, o, l, space, d, e, space, C, l, end text, start subscript, 2, end subscript, end cancel, end fraction, equals, 3, point, 99, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript

El rendimiento teórico se reporta con unidades de masa, así que podemos convertir los moles de $\text{AlCl}_3$start text, A, l, C, l, end text, start subscript, 3, end subscript a gramos usando el peso molecular:

$\text{rendimiento teórico en gramos}=3.99 \times 10^{-2}\,\cancel{\text {mol de AlCl}_3} \times \dfrac{133.33\,\text {g de AlCl}_3}{1 \,\cancel{\text {mol de AlCl}_3}}= 5.32\,\text{g de AlCl}_3$start text, r, e, n, d, i, m, i, e, n, t, o, space, t, e, o, with, \', on top, r, i, c, o, space, e, n, space, g, r, a, m, o, s, end text, equals, 3, point, 99, times, 10, start superscript, minus, 2, end superscript, start cancel, start text, m, o, l, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript, end cancel, times, start fraction, 133, point, 33, start text, g, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript, divided by, 1, start cancel, start text, m, o, l, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript, end cancel, end fraction, equals, 5, point, 32, start text, g, space, d, e, space, A, l, C, l, end text, start subscript, 3, end subscript

Rendimiento porcentual

El rendimiento téorico es la máxima cantidad de producto que podemos esperar obtener de una reacción basándonos en la cantidad de reactivo limitante. En la práctica, sin embargo, es difícil que los químicos obtengan el rendimiento máximo por varias razones. Cuando se realiza una reacción en el laboratorio se puede perder algo del producto durante la purificación o los pasos de aislamiento. Incluso puedes llegar a decidir que vale la pena perder 10% de tu producto en un paso extra de purificación porque sabes que es más importante obtener un producto extremadamente puro en lugar de tener más cantidad de un producto menos puro.

Un gato ladrón vestido de rayas y con un antifaz sosteniendo el pan robado

¡Oh, no! Un gato ladrón nos robó un pan. Eso significa que el rendimiento real es de tres perritos calientes. Si nuestro rendimiento teórico era cuatro perritos calientes, ¿cuál es nuestro rendimiento porcentual?

Sin importar qué tan ordenada y prolija parezca una reacción balanceada, los reactivos pueden reaccionar de formas inesperadas y no deseadas, incluso haciendo una reacción completamente diferente —a veces llamada reacción secundaria— que forma productos que no queremos. Tu rendimiento real puede cambiar por factores como la estabilidad relativa de los reactivos y de los productos, la pureza de los químicos usados o la humedad que había ese día. En algunos casos puedes quedarte con todos los reactivos y ningún producto al final de tu reacción. ¡Las posibilidades son inagotables!

Como los químicos ya saben que el rendimiento real va a ser menor que el rendimiento teórico, se reporta el rendimiento real usando el rendimiento porcentual, que nos dice qué porcentaje del rendimiento teórico vamos a obtener. Esta tasa puede ser muy valiosa para otras personas que quieren probar nuestra reacción. El rendimiento porcentual se determina usando la siguiente ecuación:

$\text{rendimiento porcentual} = \dfrac{\text{rendimiento real}}{\text{rendimiento teórico}} \times 100\%$start text, r, e, n, d, i, m, i, e, n, t, o, space, p, o, r, c, e, n, t, u, a, l, end text, equals, start fraction, start text, r, e, n, d, i, m, i, e, n, t, o, space, r, e, a, l, end text, divided by, start text, r, e, n, d, i, m, i, e, n, t, o, space, t, e, o, with, \', on top, r, i, c, o, end text, end fraction, times, 100, percent

Puesto que el rendimiento porcentual es un porcentaje, esperarías tener un rendimiento porcentual entre cero y 100. Si tu rendimiento porcentual es mayor a 100, probablemente calculaste o mediste algo de forma incorrecta.

Ejemplo 3: calcular el rendimiento teórico y porcentual

La siguiente reacción se lleva a cabo con 1.56g de $\text {BaCl}_2$start text, B, a, C, l, end text, start subscript, 2, end subscript, que es el reactivo limitante. Logramos aislar 1.82g del producto deseado, $\text {AgCl}$start text, A, g, C, l, end text.

$\text {BaCl}_2(ac)+2 \text{AgNO}_3(ac) \rightarrow 2\text{AgCl}(s)+\text{Ba(NO}_3)_2(ac)$start text, B, a, C, l, end text, start subscript, 2, end subscript, left parenthesis, a, c, right parenthesis, plus, 2, start text, A, g, N, O, end text, start subscript, 3, end subscript, left parenthesis, a, c, right parenthesis, right arrow, 2, start text, A, g, C, l, end text, left parenthesis, s, right parenthesis, plus, start text, B, a, left parenthesis, N, O, end text, start subscript, 3, end subscript, right parenthesis, start subscript, 2, end subscript, left parenthesis, a, c, right parenthesis

¿Cuál es el rendimiento porcentual de esta reacción?

Primero tenemos que revisar si la reacción está balanceada. Parece que tenemos el mismo número de átomos en los dos lados, por lo que podemos proceder a calcular el rendimiento teórico.

Paso 1: encontrar los moles del reactivo limitante.

Podemos calcular los moles del reactivo limitante $\text {BaCl}_2$start text, B, a, C, l, end text, start subscript, 2, end subscript usando el peso molecular:

$1.56\,\cancel{\text {g de BaCl}_2} \times \dfrac{1\,\text{mol de BaCl}_2}{208.23\, \cancel{\text{g de BaCl}_2}} =7.49 \times 10^{-3} \,\text {mol de BaCl}_2$1, point, 56, start cancel, start text, g, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript, end cancel, times, start fraction, 1, start text, m, o, l, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript, divided by, 208, point, 23, start cancel, start text, g, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript, end cancel, end fraction, equals, 7, point, 49, times, 10, start superscript, minus, 3, end superscript, start text, m, o, l, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript

Paso 2: calcular los moles de producto.

Podemos calcular cuántos moles de $\text {AgCl}$start text, A, g, C, l, end text esperaríamos tener si usamos la relación estequiométrica de la ecuación balanceada. La ecuación balanceada nos dice que esperamos obtener 2 moles de $\text{AgCl}$start text, A, g, C, l, end text por cada 1 mol de $\text{BaCl}_2$start text, B, a, C, l, end text, start subscript, 2, end subscript:

$7.49 \times 10^{-3} \,\cancel{\text {mol de BaCl}_2} \times \dfrac{2\,\text{mol de AgCl}}{1\, \cancel{\text{mol de BaCl}_2}} =1.50 \times 10^{-2} \text{mol de AgCl}$7, point, 49, times, 10, start superscript, minus, 3, end superscript, start cancel, start text, m, o, l, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript, end cancel, times, start fraction, 2, start text, m, o, l, space, d, e, space, A, g, C, l, end text, divided by, 1, start cancel, start text, m, o, l, space, d, e, space, B, a, C, l, end text, start subscript, 2, end subscript, end cancel, end fraction, equals, 1, point, 50, times, 10, start superscript, minus, 2, end superscript, start text, m, o, l, space, d, e, space, A, g, C, l, end text

Paso 3: convertir los moles de producto a gramos.

Podemos convertir los moles de $\text{AgCl}$start text, A, g, C, l, end text a la masa en gramos usando el peso molecular, lo que nos dará el rendimiento teórico en gramos:

$1.50 \times 10^{-2} \,\cancel{\text {mol de AgCl}} \times \dfrac{143.32\, \text{g de AgCl}}{1\,\cancel{\text{mol de AgCl}}}=2.15 \,\text{g de AgCl}$1, point, 50, times, 10, start superscript, minus, 2, end superscript, start cancel, start text, m, o, l, space, d, e, space, A, g, C, l, end text, end cancel, times, start fraction, 143, point, 32, start text, g, space, d, e, space, A, g, C, l, end text, divided by, 1, start cancel, start text, m, o, l, space, d, e, space, A, g, C, l, end text, end cancel, end fraction, equals, 2, point, 15, start text, g, space, d, e, space, A, g, C, l, end text

Podemos usar el rendimiento teórico y el rendimiento real para calcular el rendimiento porcentual usando la siguiente ecuación:

$\begin{aligned}\text{rendimiento procentual}& = \dfrac{\text{rendimiento real}}{\text{rendimiento teórico}} \times 100\%\\ \\ &=\dfrac{1.82 \,\text{g de AgCl}}{2.15 \,\text{g de AgCl}} \times 100\%\\ \\ &= 84.6\% \,\text{de rendimiento}\end{aligned}$

Resumen

El reactivo limitante es el reactivo que se agota primero durante una reacción y también determina cuánto producto podrá hacerse. Podemos encontrar el reactivo limitante usando las relaciones estequiométricas de la reacción junto con alguno de los ingeniosos métodos del Ejemplo 1.

Una vez que conocemos el reactivo limitante, podemos calcular la máxima cantidad de producto posible, que se conoce como el rendimiento teórico. Debido a que la cantidad real de producto casi siempre es menor al rendimiento teórico, los químicos también calculan el rendimiento porcentual usando la proporción entre el rendimiento experimental y el teórico.

    TAREA

REALICE UN MAPA CONCEPTUAL