Sistema Internacional de Unidades (SI)
El avance de la ciencia era evidente para el siglo XIX, y no hace muchos años en la ciudad de Ginebra, Suiza. Pero era necesario actualizar las unidades de medida, es por ello que surge el Sistema Internacional de Unidades (SI), este sistema tiene su esencia y base en el sistema MKS, solo que a excepción del MKS este sistema establece siete magnitudes fundamentales.
- Longitud → Metro
- Masa → Kilogramo
- Tiempo → Segundo
- Temperatura → Kelvin
- Intensidad de Corriente Eléctrica → Ampere
- Intensidad Luminosa → Candela
- Cantidad de Sustancia → Mol
Prefijos Utilizados para el Sistema Internacional
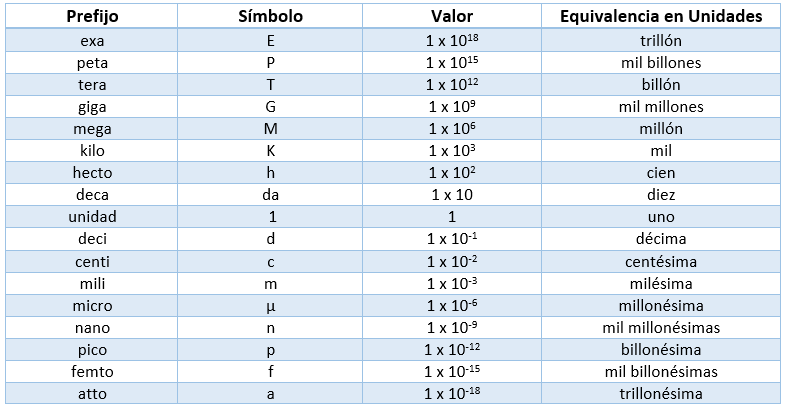
Magnitudes Derivadas
Las magnitudes derivadas son aquellas magnitudes que se pueden obtener a partir de otras magnitudes físicas, es muy común obtener magnitudes derivadas al multiplicar o dividir las magnitudes fundamentales. Veamos un ejemplo muy sencillo:
Longitud/Tiempo = m/s → (metro / segundo)
Obtenemos la velocidad a través la longitud y el tiempo, es decir a partir de las magnitudes fundamentales.
Y así podemos encontrarnos con varias magnitudes derivadas, tales como la aceleración, fuerza, trabajo, energía, presión, potencia, densidad, etc. En la siguiente imagen, se puede observar mucho mejor.

Ejercicios Resueltos de Conversión de Unidades
Es importante en Física aprender a convertir las unidades, el poder transformar unidades de un sistema a otro. Así que antes de comenzar a resolver ejercicios, veamos una tabla comparativa de equivalencias, tal como se muestra:

Veamos la siguiente conversión de unidades.
Solución: Lo primero que haremos será analizar cuántos metros caben en 1 kilómetro, y si observamos la tabla, vemos que cabe exactamente 1 000 metros, entonces aplicamos nuestro factor de conversión de tal manera que quede expresado de la siguiente manera:
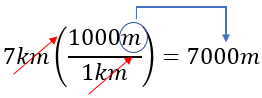
Solución: Para convertir 7 pies a metros, necesitamos verificar nuestra tabla, y observar el factor de conversión que utilizaremos. En este caso sería; 1 metro = 3.28 pies (ft)
Veamos el mismo ejemplo de forma gráfica (para darnos cuenta como se simplifican las unidades de medida).
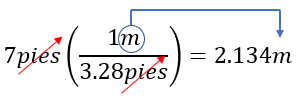
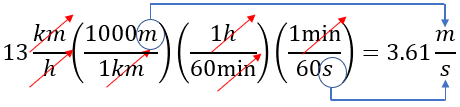
Solución: En este caso tenemos velocidad en unidades de longitud y tiempo, para ello veamos los recursos que tenemos para identificar los factores de conversión posibles. Sabemos que:
1 km = 1000 m
1 hr = 60 min
1 min = 60 s
Con estos datos podemos obtener la conversión sin problemas, ejemplo:
Aquí veamos la solución más claro, en caso que tengas dudas:
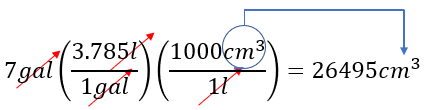
Solución: En este caso, necesitamos observar si hay alguna relación directa con el factor de conversión con galones y centímetros cúbicos, pero vemos qué no hay (en nuestra tabla), entonces tenemos que guiarnos con algo que nos pueda ayudar a relacionar dichas medidas, por ejemplo. Sabemos que:
1 Galón = 3.785 litros
1 Litro = 1000 cm³
Con estos datos, podemos obtener la respuesta. Entonces colocamos.
Veamos más claro la conversión:
Solución: Al igual que el ejemplo 3, tenemos que relacionar los factores de conversión disponibles para realizar nuestro cálculo de manera correcta, para ello comenzamos con utilizar:
1 milla = 1.609 km
1 km = 1000 m
1 hr = 60 min
1 min = 60 s
Ahora si podemos realizar la conversión
Para ver más clara la conversión, veamos la imagen:

TAREA
REALICE DOS EJERCICIOS DE LOS PROPUESTOS
![]()
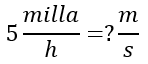
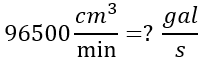
![]()
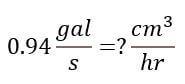
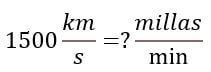

muchas gracias , me sirvió mucho este blog
ResponderEliminar