Conversión de Unidades de medida:Ejemplos, Problemas y Test |
-
Introducción
-
1. Conceptos Básicos
-
2. Longitud (metros)
-
3. Área (metros cuadrados)
-
4. Volumen (litros)
-
5. Volumen (metros cúbicos)
-
6. De litros a metros cúbicos
-
7. Tiempo (segundos)
-
8. Masa (gramos)
-
9. Problemas Resueltos y Test
Introducción
Comentaremos un par de ejemplos para comprender la necesidad y las razones de las conversiones entre las unidades de medida:- En la astronomía, las distancias son extremadamente grandes.
Por ejemplo, tan sólo la distancia del Sol a la Tierra es de unos
150 000 000 kilómetros.Y el diámetro del supercúmulo de Virgo es de unos
1 892 146 200 000 000 000 000 kilómetros. - En la química nuclear, la distancia media entre dos núcleos de
carbono es aproximadamente
0.000000000154 metros.
Básicamente, por estas razones, para cada magnitud (longitud, área, volumen, intensidad...) tenemos varias unidades que son múltiplos (o submúltiplos) de la unidad básica (la del SI).
Por ejemplo, podremos decir
-
10 kilómetros (10 km)
en lugar de 10 mil metros (10000 m); ó
- 3 horas (3 h) en lugar de
10800 segundos (10800 s).
1. Conceptos Básicos
Magnitud, medición, unidad de medida, Sistema Internacional de Unidades (SI)...

Ver Conceptos
Ahora vamos a ver cómo pasar de una unidad de medida a otra. Por ejemplo, de metros a kilómetros o de metros cúbicos a litros.
La regla que emplearemos para cambiar de unidades es:
«Multiplicar para Bajar
y
Dividir para Subir»
2. Unidades de Longitud (metros)
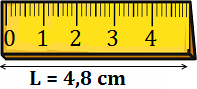
Ver Escala y Ejemplos
3. Unidades de Área (metros cuadrados)

Ver Escala y Ejemplos
4. Unidades de Volumen (litros)
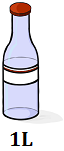
Ver Escala y Ejemplos
5. Unidades de Volumen (metros cúbicos)
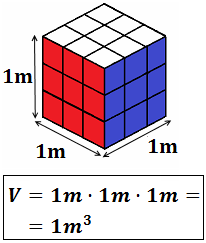
Ver Escala y Ejemplos
6. De metros cúbicos a litros y viceversa (unidades de volumen)
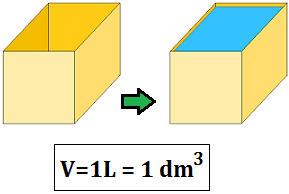
Ver Equivalencia
7. Unidades de Tiempo (segundos)
Ver Escala
8. Unidades de Masa (gramos)

Ver Escala y Ejemplos
9. Problemas Resueltos y Test
9.1 Problemas
Problema 1: unidades de longitudEscribir las siguientes distancias en metros:
- 15 km
-
200 dm
- 23 mm
- 0,02 dam
- 2 cm
Ver solución
Problema 2: unidades de longitud
Escribir las siguientes longitudes en decámetros realizando un solo paso (multiplicando/dividiendo sólo una vez):
- 11 mm
- 5 hm
-
0,05 dm
Ver solución
Recordamos la escala métrica:
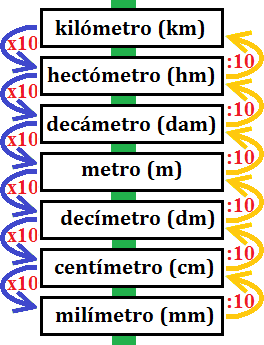

- 11 mm
Para pasar de milímetros a decámetros tenemos que subir 4 escalones. Por tanto, tenemos que dividir 4 veces entre 10. Podemos realizar estas 4 divisiones dividiendo una sola vez por 104 = 10000:
Si queremos evitar los decimales podemos usar notación científica: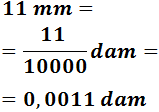
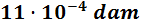
- 5 hm
Para pasar de hectómetros a decámetros tenemos que bajar un escalón:
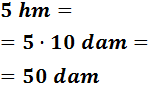
- 0,05 dm
Para pasar de decímetros a decámetros tenemos que subir dos escalones. Por tanto, dividir dos veces entre 10, que es lo mismo que dividir entre 102 = 100:
En notación científica: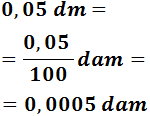
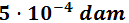
Problema 3: unidades de área
Escribir las siguientes áreas en decímetros cuadrados:
- 13 mm2
- 200 dam2
- 0,0000003 km2
Ver solución
Recordamos la escala de metros cuadrados:
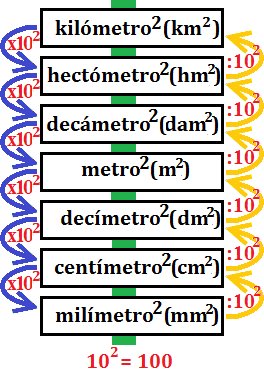

- 13 mm2
Para pasar de milímetros a decímetros tenemos que subir 2 escalones.
Como estamos trabajando con áreas, tendremos que dividir dos veces entre 102 = 100:
En notación científica: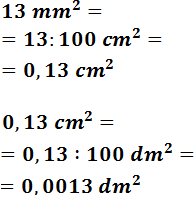
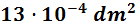
- 200 dam2
Para pasar de decámetros a decímetros tenemos que bajar (multiplicar) 2 escalones.
Multiplicamos 2 veces por 100:
En notación científica: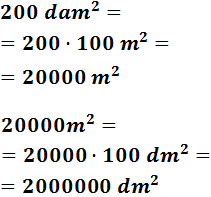
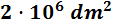
- 0,0000003 km2
Para pasar de kilómetros a decímetros tenemos que bajar 4 escalones.
Por tanto, multiplicamos 4 veces por 100:
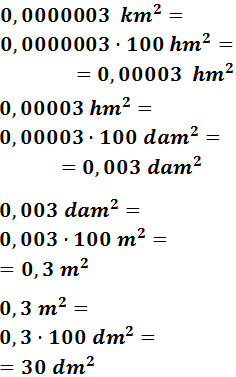
Problema 4: unidades de área
Escribir las siguientes áreas en kilómetros cuadrados multiplicando o dividiendo sólo una vez:
- 1,3 dam2
- 0,12 hm2
- 5 mm2
Ver solución
Recordamos la escala de metros cuadrados:


- 1,3 dam2
Para pasar de decámetros a kilómetros tenemos que subir 2 escalones. Por tanto, tenemos que dividir dos veces entre 100.
Dividir dos veces entre 100 es lo mismo que dividir una vez entre 10000:
En notación científica: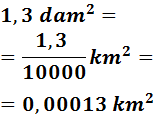
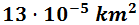
- 0,12 hm2
Como tenemos que subir 1 escalón, dividimos una vez entre 100:
En notación científica: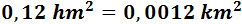
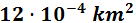
- 5 mm2
Tenemos que subir 6 escalones, lo que supone dividir 6 veces entre 100. Esto es lo mismo que dividir una vez entre 1006.
Además, notemos que podemos escribir
De este modo,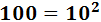
Escribimos directamente en notación científica porque tenemos demasiados ceros: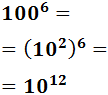
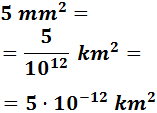
Problema 5: unidades de volumen
Escribir las siguientes medidas en litros:
- 2,3 ml
- 4,1 kl
- 2 dal
- 3 m3
-
0,005 km3
- 9 mm3
Ver solución
La escala de los litros es:
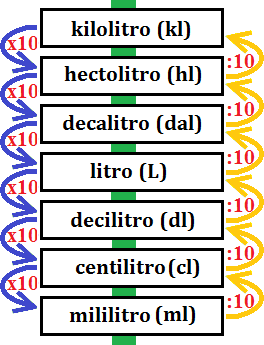

- 2,3 ml
Para pasar de mililitros a litros tenemos que subir 3 escalones:
En notación científica: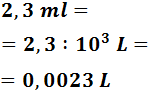
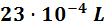
- 4,1 kl
Para pasar de kilolitros a litros tenemos que bajar 3 escalones:
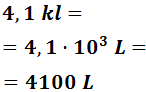
- 2 dal
Para pasar de decalitros a litros tenemos que bajar 1 escalón:
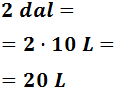
- 3 m3
Como tenemos el volumen en metros cúbicos, tendremos que usar la relación
Pasamos a decímetros cúbicos (bajamos 1 escalón) y ya tendremos las unidades en litros: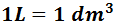
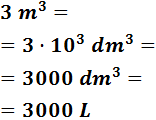
- 0,005 km3
Bajamos 4 escalones:
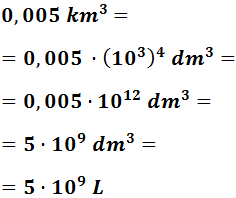
- 9 mm3
Subimos 2 escalones:
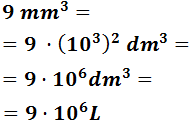
Problema 6: unidades de tiempo
Escribir las siguientes medidas en minutos:
- 3 horas
- 2 días
- 2 meses
- 1980 segundos
Ver solución
- 3 horas
Para pasar de horas a minutos tenemos que multiplicar por 60:
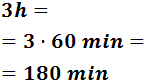
- 2 días
Un día son 24 horas y una hora son 60 minutos:
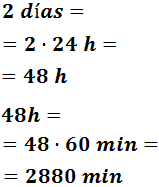
- 2 meses
Un mes son 4 semanas; 1 semana son 7 días; 1 día son 24 horas; y 1 hora son 60 minutos:
Multiplicamos por 4 para pasar de meses a semanas:
Multiplicamos 7 para pasar de semanas a días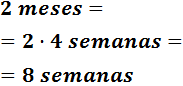
Multiplicamos por 24 para pasar de días a horas
Multiplicamos por 60 para pasar de horas a minutos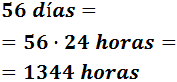
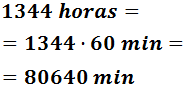
- 1980 segundos
Un minuto son 60 segundos. Por tanto, para pasar de segundos a minutos tenemos que dividir entre 60:
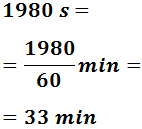
Problema 7: unidades de tiempo
Escribir los siguientes tiempos en días:
- Un año y medio
- 2 trimestres
- Un sexenio
- Dos octavarios
- 259200 segundos
- 1440 minutos
Ver solución
- Un año y medio
Un año son 365 días y, por tanto, un año y medio son
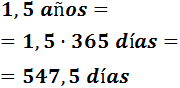
- 2 trimestres
1 trimestre son 3 meses; un mes son 28 días.
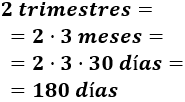
- Un sexenio
Un sexenio son 6 años.
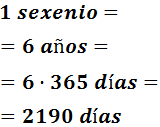
- Dos octavarios
Un octavario son 8 días.
Por tanto, dos octavarios son 16 días.
- 259200 segundos
Pasamos a minutos:
Pasamos a horas: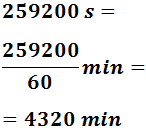
Pasamos a días: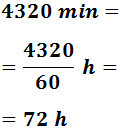
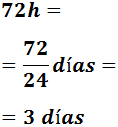
- 1440 minutos
Pasamos a horas y después a días dividiendo entre 60 y entre 24:
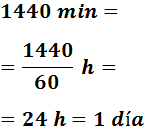
Problema 8
Calcular cuántos litros de agua caben en una piscina de dimensiones 3x6x23 m.
Ver solución
Problema 9
Calcular los litros de agua que caben en un recipiente esférico de cristal de radio 0,2 metros.

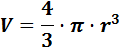
Ver solución
El radio es 0,2 metros, es decir, 2 dm.
Sabemos que el volumen de una esfera es
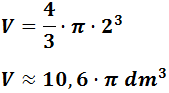 Aproximando π = 3,14159 :
Aproximando π = 3,14159 :
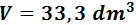 El volumen lo tenemos en decímetros cúbicos porque hemos escrito el radio en decímetros.
El volumen lo tenemos en decímetros cúbicos porque hemos escrito el radio en decímetros.
Por tanto, se necesitan, aproximadamente 33,3 L (porque 1L = 1dm3).
Sabemos que el volumen de una esfera es
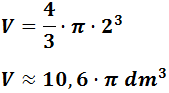
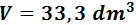
Por tanto, se necesitan, aproximadamente 33,3 L (porque 1L = 1dm3).
Problema 10
Calcular la masa total de un bidón metálico de 1kg con forma cilíndrica de 1 metro de radio y 2 metros de altura lleno de agua.
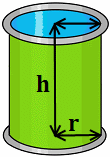
Ver solución
9.2 Test
En todas las preguntas, escoger la opción correcta.
Pregunta 1
Para medir la longitud de una cuerda emplearemos la unidad de medida...
|
Metros.
|
|
|
Metros cuadrados.
|
|
|
Metros cúbicos.
|
Mostrar
El metro cuadrado es una unidad de medida de áreas y el metro cúbico, de volumen.
Pregunta 2
Para medir el volumen del líquido de un recipiente cilíndrico podemos usar la unidad de medida...
|
Metros cuadrados.
|
|
|
Metros cúbicos.
|
|
|
Metros cilíndricos.
|
|
|
Todas las opciones anteriores son verdaderas.
|
Mostrar
Usaremos metros cúbicos ya que es la unidad de medida de volumen.
La forma de un objeto no interviene en su volumen. Por ejemplo, un litro de agua ocupa lo mismo en una botella que en una jarra, aunque en una forma distinta.
La forma de un objeto no interviene en su volumen. Por ejemplo, un litro de agua ocupa lo mismo en una botella que en una jarra, aunque en una forma distinta.
Pregunta 3
Para saber la pintura necesaria para pintar un muro tenemos que medir...
|
La longitud del muro.
|
|
|
El área del muro.
|
|
|
El volumen del muro.
|
Mostrar
Tenemos que medir el área.
Si sabemos sólo la longitud del muro no podemos calcular la pintura necesaria ya que la altura del muro también es un factor a considerar.
Si sabemos sólo la longitud del muro no podemos calcular la pintura necesaria ya que la altura del muro también es un factor a considerar.
Pregunta 4
Las unidades de kilómetros, hectómetros y decámetros son...|
Submúltiplos del metro.
|
|
|
Múltiplos del metro.
|
|
|
Las dos opciones anteriores son verdaderas.
|
Mostrar
Pregunta 5
1 metro son 10 decímetros y 1 metro cuadrado son...|
10 decímetros cuadrados
|
|
|
100 decímetros cuadrados
|
|
|
Ninguna de las anteriores.
|
Mostrar
En la escala de los metros (longitud), para pasar de metros a decímetros multiplicamos por 10.
En la escala de los metros cuadrados (área), para pasar de metros cuadrados a decímetros cuadrados multiplicamos por 102 = 100.
En la escala de los metros cuadrados (área), para pasar de metros cuadrados a decímetros cuadrados multiplicamos por 102 = 100.
Pregunta 6
Para pasar de horas a segundos tenemos que...|
Multiplicar por 60.
|
|
|
Dividir por 3600.
|
|
|
Multiplicar por 3600.
|
Mostrar
Para pasar de horas a minutos multiplicamos por 60 y para pasar de minutos a segundos multiplicamos
por 60.
Por tanto, para pasar de horas a segundos tenemos que multiplicar dos veces por 60, que es lo mismo que multiplicar una vez por 3600.
Por tanto, para pasar de horas a segundos tenemos que multiplicar dos veces por 60, que es lo mismo que multiplicar una vez por 3600.
Pregunta 7
Dos milenios y medio son...|
Trescientos siglos.
|
|
|
Veinticinco lustros.
|
|
|
Doscientas cincuenta décadas.
|
Mostrar
Como un milenio son 1000 años, dos milenios y medio son 2500 años.
Una década son 10 años.
Por tanto, 250 décadas son
Una década son 10 años.
Por tanto, 250 décadas son
años.
Pregunta 8
Un trimestre son...|
Dos meses.
|
|
|
Tres meses.
|
|
|
Trece días.
|
Mostrar
El prefijo tri- significa tres.
Un trimestre son 3 meses.
Un trimestre son 3 meses.
Pregunta 9
Un sexenio son...|
6 días.
|
|
|
6 meses
|
|
|
6 años.
|
Mostrar
Un sexenio son 6 años.
No existe vocablo para el período de 6 días (casi una semana).
El período de 6 meses se denomina semestre.
No existe vocablo para el período de 6 días (casi una semana).
El período de 6 meses se denomina semestre.
Pregunta 10
Un decisegundo son 0,1 segundos; 1 decisegundo son 10 centisegundos.Entonces, 3 segundos son ...
|
0,3 decisegundos
|
|
|
0,3 centisegundos
|
|
|
300 centisegundos
|
Mostrar
Para pasar de segundos a decisegundos multiplicamos por 10 y para pasar de
decisegundos a centisegundos también.
Por tanto, 3 segundos son 300 centisegundos.
Por tanto, 3 segundos son 300 centisegundos.
No hay comentarios:
Publicar un comentario