Diámetro de la tierra
Los tamaños de los diversos cuerpos del sistema solar son muy
distintos. El Sol es mucho más grande que la Tierra, y ésta es varias
veces mayor que la Luna. Hacer modelos que sigan esas mismas
proporciones nos llevará a comprender mejor su tamaño. La tierra tiene
unos 13.000 km de diámetro y la luna 3.500 km. Por tanto,
el diámetro de la tierra es unas cuatro veces el de la luna.
Como sabemos todos, la tierra no es plana sino que tiene forma
esférica, medir una Tierra plana ya en sí hubiera sido un grandísimo
trabajo, pero una Tierra esférica produce efectos que dependen del
tamaño de la esfera.
Si la Tierra fuese enorme, los efectos de su esfericidad serían tan
pequeños que no se podrían detectar de una forma sencilla como por
ejemplo los barcos no desaparecían tras el horizonte cuando el
observador todavía viese una imagen tan grande, ni se vería cómo primero
se oculta el casco y luego la vela.
Si los efectos de la esfericidad eran perceptibles quería decir
que la Tierra era una esfera, pero también una esfera de tamaño
moderado.
Medir el diámetro de la Tierra
Si
conocemos la circunferencia de una esfera, podremos conocer también su
diámetro, tal y como Eratóstenes calculó así que la Tierra tenía una
circunferencia de unos 40.000 kilómetros y un diámetro de unos 12.800
kilómetros
El planeta Tierra es una esfera ligeramente aplastada en los polos. Su
superficie es de unos 510 millones de kilómetros cuadrados y la longitud
de su radio oscila entre 6357 km (radio polar) y 6378 km (radio
ecuatorial). La forma de la Tierra y de los otros planetas no es la de
una esfera sino la de un esferoide aplastado por los polos debido al
movimiento de rotación alrededor de sus ejes.
El diámetro de la Tierra fue medido por primera vez por Eratóstenes.
Esta medida fue obtenida sin que él saliera de la biblioteca en la que
trabajaba, ubicada en la
ciudad de Alejandría,
en el norte de Egipto, entre 276 a. C y 196 a. C. Eratóstenes era el
responsable de la biblioteca del museo, había muchos intereses sobre las
ciencias y escuchó los comentarios de los viajeros que habían estado en
la ciudad de Siene, donde se encuentra hoy la presa de Assuam, y donde
exactamente al medio día del primer día de verano (21 de junio), el Sol
se ponía sobre las cabezas de las personas, la conducción de los rayos
de una forma vertical. Mirando un pozo profundo, se podía ver el reflejo
del Sol en el fondo del pozo. Eratóstenes observó que en este mismo día
y hora en Alejandría había una sombra provocada por los rayos solares
que no estaba siendo producida verticalmente, pero formando un ángulo un
poco mayor que 7° en relación a la ciudad de Siene que quedaba 800Km
más al Sur.
Partiendo de esta información y teniendo en cuenta que muchas de las
medidas de la época eran imprecisas, Eratóstenes calculó el diámetro de
la Tierra haciendo el siguiente análisis:
Si una circunferencia tiene 360° y un desplazamiento angular de 7°
corresponde a aproximadamente 1/50 de un círculo y esta medida en grados
equivale a 800Km, entonces la vuelta completa debe coincidir con el
diámetro de la Tierra, que deberá ser aproximadamente 800×50Km=40.000
Km.
Cómo Erastósenes calculó el diámetro de la Tierra
Actualmente, sabemos el diámetro de la Tierra mide 39.830 Km y observamos que la medida obtenida para la época era excelente.
Observamos que el simple análisis de una regla de tres simple y
directa permitió tal cálculo junto con otra idea matemática de que la
proyección de los rayos solares puede ser observada a través del montaje
de un triángulo rectángulo y la medida del diámetro puede ser calculada
sin el acceso real al lugar de la medida. Aquí nos damos cuenta de la
importancia de los conceptos de trigonometría y de semejanza de
triángulos.
Últimos estudios sobre el diámetro de la Tierra
Cabe añadir que en los últimos estudios realizado por un equipo de
científicos de la Universidad de Bonn (Alemania, oeste) se ha podido
demostrar que
el diámetro de la Tierra es 5 milímetros más pequeño de lo que se creía hasta ahora.
Un grupo de investigadores del Instituto geodésico de la universidad ha demostrado que
el
diámetro de la Tierra, de 12.756,274 kilómetros, es en realidad 5
milímetros más pequeño de lo establecido en la última medición, efectuada hace años, precisó a la AFP Axel Nothnagel, que dirige el equipo.
Aunque la diferencia pueda parecer nimia para el gran público,
resulta muy importante para el estudio de los cambios climáticos.
“Parece una diferencia insignificante, pero es fundamental para el
posicionamiento de los satélites capaces de medir la elevación del nivel
de los océanos”, explicó Nothnagel.
Los investigadores también descubrieron que Europa y el continente
norteamericano se separan 18 milímetros cada año. Y hasta aquí nuestra
información sobre el
diámetro de la Tierra.
La primera idea de medir la Tierra. El método del meridiano
Una vez que los griegos descubrieron que la Tierra tenía forma
esférica, se pusieron a imaginar artificios para determinar el tamaño de
esa esfera.
En ese sentido, la primera idea que surgió fue la de
reducir el problema de la determinación del tamaño de la Tierra a un problema de geometría plana.
La estrategia más sencilla de obtener dicha reducción era la de hacer
medidas en un mismo meridiano, método que explicaremos en detalle a
continuación.
¿Qué es un meridiano?
Suponiendo que la Tierra es una esfera perfecta, los
meridianos terrestres son los círculos que apuntan al centro de la Tierra y pasan por los dos polos.
La prolongación de estos círculos hasta la esfera celeste da los llamados meridianos celestes.
Paralelos y meridianos
El
meridiano terrestre que pasa por un determinado lugar sobre la
superficie de la Tierra, y el correspondiente meridiano celeste, son
llamados meridianos locales.
Utilidad del meridiano celeste de un determinado lugar:
- contiene el cenit del lugar ( = punto en que la vertical del lugar “pega” con la esfera celeste )
- en su viaje diario a través de la esfera celeste, el Sol alcanza su
posición más alta (= dando su menor sombra) en tal lugar cuando se cruza
en su meridiano celeste.
¿Cómo podemos encontrar el meridiano de un lugar sobre la superficie de la Tierra?
Si clavamos verticalmente una varilla en el suelo, la dirección de la
sombra mínima producida por esta varilla a lo largo de un día es la
dirección del meridiano local.
Algunas peculiaridades griegas
Los griegos expresaban el tamaño de la Tierra dando el valor de la
circunferencia de los meridianos terrestres y no en términos del radio o
diámetro de la Tierra. La razón era simple: podemos calcular la
circunferencia usando el razonamiento de proporciones, mientras que la
determinación del radio o diámetro, a partir de la circunferencia,
implica el conocimiento del valor numérico de PI, con varias cifras
decimales.
.
Presión inicial
Volumen Inicial
Presión Final
Volumen Final
.
átomos
de S
átomos
de K
átomos
Na
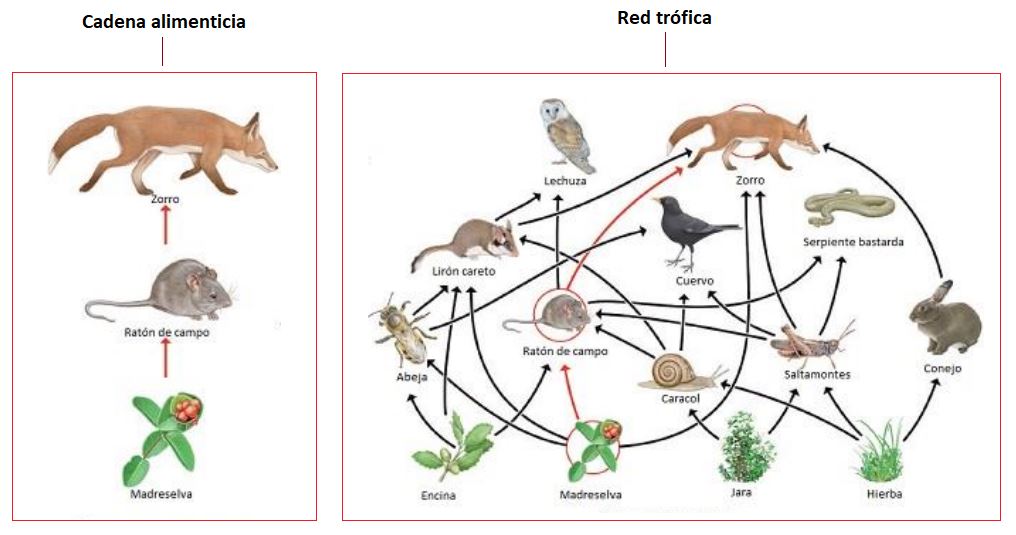
Es
importante señalar que a lo largo del paso por la cadena trófica se
genera una gran pérdida de energía, a medida que ésta se transfiere de
un